Quantum instanton evaluation of kinetic isotope effects
Kinetic isotope effect (KIE) is the effect of an isotopic substitution on the rate constant,
KIE = klight / kheavy.
We have implemented a method (Vanicek et al 2005a,Vanicek and Miller 2007,Zimmermann and Vanicek 2010,Vanicek 2011,book chapter] to compute the KIE based on the quantum instanton (QI) approximation for the thermal rate constant [W. H. Miller et al. 2003], on thermodynamic integration (TI) with respect to the isotopic mass, and on the path integral Monte Carlo (PIMC) evaluation. As a first test, our method correctly reproduced KIEs in various isotopic variants of the simplest hydrogen exchange reaction (Vanicek et al 2005a). Later we made the method much more efficient (by deriving alternative estimators to make the statistical error independent of the number of imaginary time slices in the path integral) (Vanicek et al 2005b) and applied it to the [1,5]-sigmatropic hydrogen shift in cis-pentadiene (see figure below) (Vanicek and Miller 2007).
 |
 |
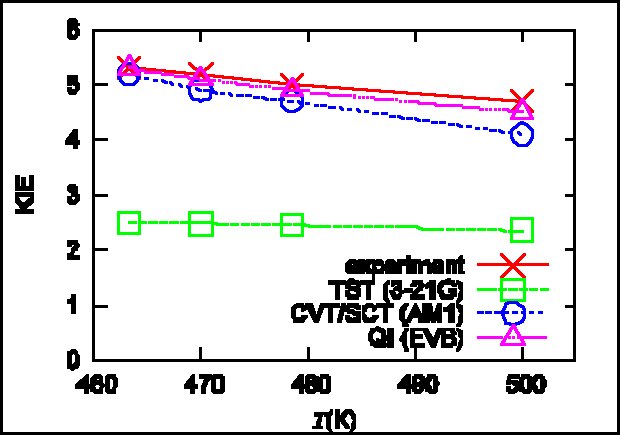 |
Recently, in collaboration with Markus Meuwly’s group at University of Basel, we calculated the KIE in malonaldehyde (MA). Specifically, we combine a fully dimensional and validated PES based on molecular mechanics with proton transfer (MMPT) with the path integral Monte Carlo (PIMC) methodology in order to determine the primary H/D KIE on the intramolecular proton transfer in MA at various temperatures (Huang et al 2013).
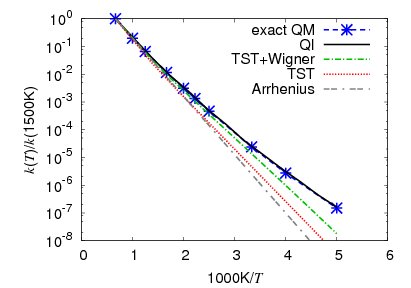
Deviations from the Arrhenius law due to quantum effects
Every respectable student of physical chemistry knows the Arrhenius law for the temperature dependence of the rate constant. In our group, we study deviations from the Arrhenius law due to tunneling and other quantum effects. Specifically, we have developed a method, based on Miller’s Quantum Instanton (QI) approximation and on the thermodynamic integration with respect to the inverse temperature, to compute the temperature dependence of the rate constant directly (Zimmermann and Vanicek 2010,1Buchowiecki and Vanicek 2010). The figure below compares our QI result with the exact quantum (QM) calculation as well as with the transtion state theory (TST) and with the Arrhenius law for the full nine-dimensional hydrogen exchange reaction H+H2→H2+H. The inaccuracies of the Arrhenius equation and of the TST (even with the Wigner tunneling correction) caused by tunneling at lower temperatures are clearly visible: