Path integral evaluation of the equilibrium isotope effects
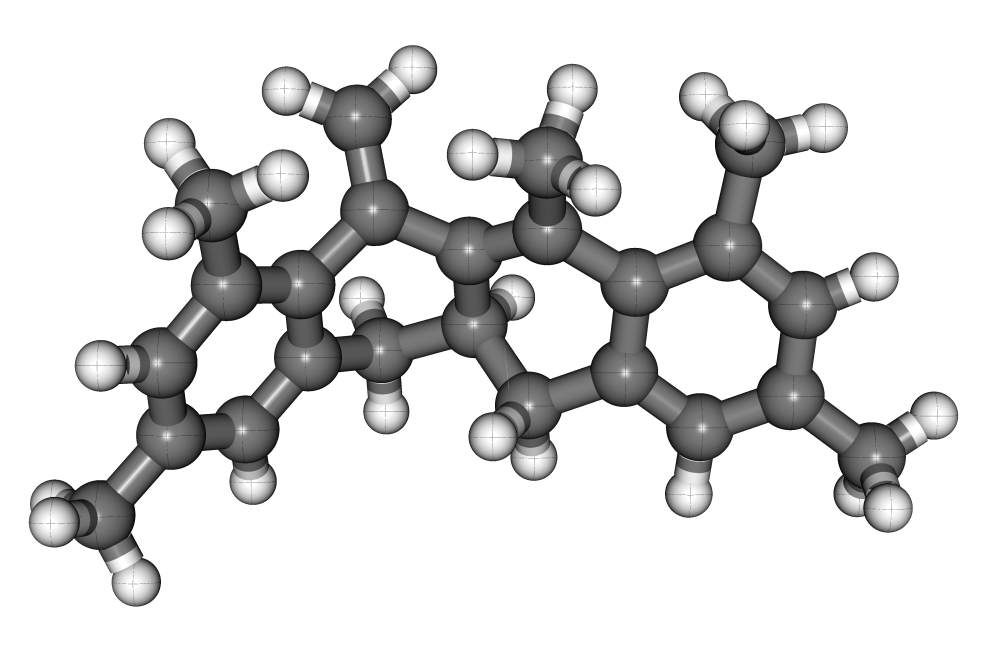
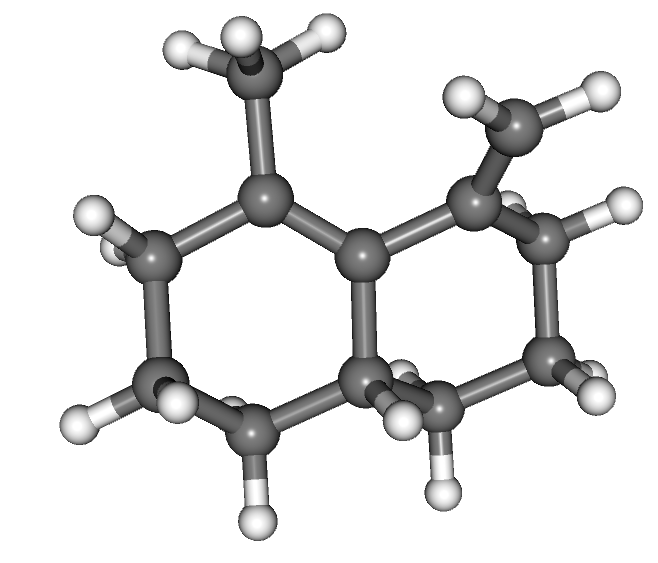
We have developed and tested a general methodology to compute the quantum equilibrium isotope effect (EIE) (Zimmermann and Vanicek 2009,Zimmerman and Vanicek 2010,Vanicek 2010). Unlike standard approaches, ours does not assume separability of rotational and vibrational motions and does not make the harmonic approximation for vibrations or rigid rotor approximation for the rotations. In particular, zero point energy and anharmonicity effects are described correctly quantum mechanically. The approach uses thermodynamic integration with respect to the mass of isotopes, Feynman path integral representation of the partition function, an efficient estimator for the derivative of free energy, and a combination of ab initio and semiempirical electronic structure methods. We have tested the method on three [1,5] sigmatropic hydrogen shift reactions. Our calculations have shown that the anharmonicity effects amount up to 30% of the symmetry reduced reaction free energy. Comparison of the numerical results with recent experiments of Doering and coworkers, has confirmed the accuracy of the most recent measurement on 2,4,6,7,9-pentamethyl-5-(5,5-2H2)methylene-11,11a-dihydro-12H-naphthacene (left figure) as well as concerns about compromised accuracy, due to side reactions, of another measurement on 2-methyl-10-(10,10-2H2 methylenebicyclo[4.4.0]dec-1-ene (right figure). The method has also been implemented in Amber since version 10 [Amber 10].
For details, see: T. Zimmermann and J. Vanicek: “Path integral evaluation of equilibrium isotope effects,” J. Chem. Phys. (2009).
Recently, we proposed an accelerated path integral approach based on three ingredients: the fourth-order Takahashi-Imada factorization of the path integral, thermodynamic integration with respect to mass, and centroid virial estimators for relevant free energy derivatives. While the first ingredient speeds up convergence to the quantum limit, the second and third improve statistical convergence (Buchowiecki and Vanicek 2013).